hatena0006

アメリカの物理学者のアラン・ソーカルという人が、経済学などにむやみやたらに数学を不正確に濫用しているのに腹を立て、逆にこんな題名の論文を寄稿しました。「量子力学の理論も社会的なコンテクストによって決定されている」という主張をデッチあげたのです。ところがその論文が学術論文の審査を通って採用されてしまいました。ソーカルは、そのいきさつを暴露してしまい、いかにデタラメであったかを見抜けなかった学術誌の編集者を厳しく批判したのですから、さあ大変！これが世にいうソーカル事件なのです。この事件は後を引き、主として槍玉に挙げられたフランスのポスト・モダン界で、議論が沸騰しました。ソーカルに賛成する人は、知的ペテンを暴いたとし,言説のパロディ、大胆ないたずら、かっこいいスタイルに引っかかった多元文化主義的人文科学への挑戦、と捉えます。これに対して、ソーカルのような人は、知識人の裏切りだとして反論します。あるいは言葉遊びにふけっているものだと非難します。言説の枝葉末節だけを批判しても何にもならない、要は思想の内容だと・・・侃々諤々。

いやいや、異論・反論・オブジェクションの喧騒さ！どうしても結論が欲しいあなたには次の言葉をもって締めましょう。

思い出そうではないか。ずいぶん昔のことだが、ある国では、思想家や哲学者たちが豊かな科学的教養に触発されて明晰に思考し、明快に書き、かつ得た知識を同国市民のあいだに広めようとしていた。その時代は啓蒙の時代であり、その国はフランスであった。（堀茂樹）

ところでこれほどの衝撃？を与えたにも拘わらず、日本でそれほど話題にならない？とは、平和で寛容な姿勢と褒めるべきか、無関心と非難すべきか、それともハテナが知らないだけかもしれませんﾈ。

（参考：稲葉振一郎　『経済学という教養』　　堀茂樹　「きみはソーカル事件を知っているか？」（http://www.gakushuin.ac.jp/~881791/fn/Hori.html)）

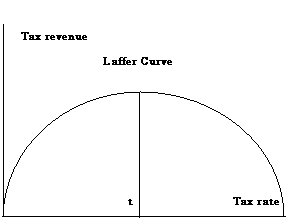
今夜はラッファー・カーブのお話。アメリカの経済学者アーサー・ラッファーという人が、時は1970年代後半、ある夜のレストランで仲間たちと談笑していたとき、手元にあったナプキンに何やら下のようなカーブを書いて説明しました。

この図は税率を単に上げただけでは税収は増加せず、それどころか t 点より右側になると、却って税収は下がることを示すものでした。余り税率を高くすると勤労する意欲がなくなるからです。したがって税率を下げ、図の t 点のところで税収は最大になるというものでした。この考えがアメリカのレーガン大統領の減税政策として採用されたものです。

わずか一枚のナプキンに描かれたこの簡単な図は、経済理論としても経済政策としても、大きな波紋を生じ、さまざまな議論を巻き起こしましたが、結局は、現行の税率が t 点より右側にあるか左側にあるかの判断と、税率の上げ下げに仕事が上の図のように感応するのか、という問題にあったわけです。

実際にはレーガンの減税は、政府支出の増大とともに大きな政府赤字を残し、かの有名なラッファーカーブはいつの間にか忘れられてしまったようです。

（参考：フリー百科事典『ウィキペディア』ラッファー曲線）

国際経済を考える上で最も簡潔な等式は、

貯蓄ー投資＝輸出ー輸入

で、これは恒等式であります。今開発経済の分野では次のような意見がよく聞かされます。例えば、最近のアジア危機などを思い起こしてください。欧米諸国から低賃金国に資本が流入する現象を捉えてみましょう。低賃金国は、そのため、国内の貯蓄以上に投資ができます（上式の左辺はマイナスです）。同時に低賃金国では賃金が低いため輸入より輸出の方が有利と考えられ、また先進工業国内で空洞化が進むと懸念する声が高まります（ということは上式の右辺はプラスです）。アレッ！上式はマイナス＝プラスとなる？？

これをどう説明できるでしょうか？　資本が低賃金国に流入すると、その国の生産性が上昇して賃金も上がるはずです。それが貯蓄となって投資を上回ることになりますと、左辺ははじめてプラスに転じます。すると今まで低賃金であったための輸出ー輸入の差も少し不利にはなりますが、依然としてプラス。そこでこの恒等式は成立します。

低賃金国が大幅な輸出超過（右辺のプラスが大）を続けるとしたら、左辺もプラス大となるはず。ということは低賃金国が高賃金国に資本を輸出するようになる！　そんなことあり？？　そんな難しいリクツを言うからお前はダメなんだ！！　けれども低賃金国が貿易黒字を出しながら、資本が流入してくる状況は、上の恒等式からあり得ないとハテナは思うんですが・・・。

（参考：ポール・クルーグマン　『クルーグマンの良い経済学悪い経済学』　原題はPop　Internationalism）

友の会ホームページに「低山を歩く会」という楽しいコンテンツがあります。これとは全く関係はないのですが、ハイキングに行くときの経済学をパロディ風に考えてみましょう。

さて、明日（仮定の話）は楽しみにしていた低山のハイキングです。それに備えてルックサックの中にどんな品物を用意すれば良いのでしょうか。大抵は、スーパーで好みの品や必要な携帯品を2～3時間もあれば整えることでしょう。ペットボトルは水にしようかお茶にしようか。雨に備えて簡単な合羽を持っていこう。寒さを癒すため或いは頂上で祝杯を挙げるにはウィスキーがいいかそれとも日本酒にしようか。お小遣いも限られているので安い方にしよう、とか・・・。

これを経済学ではどう取り扱うのでしょうか。まず二つの出発点を想定します。一つはお小遣いの限度があるということで、これを予算制約条件といいます。もう一つはその予算のなかで最も適った品物を選ぶということで、これを効用を最大化するといいます。これらを合わせて、予算制約下の効用最大化問題としてルックサックの中身を解く、ということになりましょう。ところが中に収める品物が2,3種類なら簡単ですが、品物の数が増えますと、案外厄介な計算を要します。人間の頭脳はこの計算を一瞬に判断して行動する素晴らしい機能をもっております。ただその品物選びが最高の満足を得られるかとうか（例えばうっかり忘れてしまった）、また同行する仲間のリックサックはそれぞれ中身が違うでしょう（人間の効用は主観的です）。経済学ではあなたの効用を比較することから始めます。例えば、品物購入予算を1万円としましょう（チョット贅沢？）。そして上の例のペットボトルを天然水とお茶のどちらを好むか比較するわけです。もちろんこの限りでは、予算の範囲内にありますね。ところが段々品数が増えていきますと計算が厄介になってきます。水とお茶のほかにコーヒーもどうか、と3品の比較に拡張しても計算はそれほど難しくない。考え方としては水とお茶の効用を比較し次いで水とコーヒの効用を比較しやはり水にしよう、と効用を選択すれば、水に決まります。ところが水とお茶、お茶とコーヒー、コーヒーと水の三通りの比較をしなくてはなりません。水よりはお茶、お茶よりはコーヒー、コーヒーよりは水と選択が異なれば堂々巡りになってしまいますね。いずれも安い品ですから、予算1万円のなかで問題はありませんが、品物がだんだん増えていきますと。お小遣いのほうも考えねばなりませんね。

人間の頭脳はこれらを苦もなく一瞬に判断しますね。そうでなければ低山歩きに参加できない！ところが経済学的にこの効用の比較をコンピュータで計算させますと、途中をはぶき、結果だけでは凡そ次のようになってしまいます。品物の数をｎとしますと、

品物の数	計算時間
n＝10 のとき	0.001秒
n＝20 のとき	1.0秒
n＝30 のとき	17.9分
n＝40 のとき	12.7日
n＝50 のとき	35.7年

となります。低山歩きに50もの品物を用意することはまずないでしょうが、仮にそうしますと、何と35年以上もかかる！普通は多くても30品目位でしょうから、18分弱とまあリーズナブルでしょう。

このコンピュータによる計算問題を有用と見るかどうかは人によって異なるでしょうが、以前ではとても解けなかった問題が段々と現実してきたことは、将棋や碁のソフトと同じように随分と進歩したとは言えるでしょう。経済学ではこのような計算量の理論を、ナップザック問題と呼んでいます。

（参考：塩沢由典　『市場の秩序学』）

経済学、とくに「厚生経済学」の諸著作でよくお目にかかるのは、「パレート最適」という言葉です。自由な市場経済では取引しようとする当事者たちはそれぞれ自分たちの利益を求めて市場に参加しています。皆が期待どうりにうまくいけば、参加者全員が以前にくらべ改善します。これをさらに突き進めていきますと、少なくとも一人については改善するがそのことによって残りの者たちが悪化しなければ、経済学者はこう言います。「市場経済における自由な取引は、社会の状態をパレートの意味で改善する」と。さらに進んで誰かが改善することによって一人でも他の人が悪化することのないところまで、行き着きます。誰かが悪化すればパレートの意味で完全とは言いません。一人でも悪化しないような極限まで改善することを、「それ以上パレート改善の余地がない」という意味で「パレート最適」と呼ぶのです。

パレート（Vilfredo Pareto）（1848～1923）は、イタリア系の経済学者のみならず、政治学、社会学の基礎原理の形成に大きな影響を与えました。

ただ、この最適問題では依然として不平等が解消されるわけではありません。確かに富者の富は貧しい者から搾取しておりません。富者がより豊かになったからといってそのせいで貧者が貧しくなることもなく、かえってそれにつられて貧者がより豊かになることもありえましょう。しかしこの考えは不平等を是認しているといえるでしょう。ということは市場経済そのものが不平等それ自体を回避できないのです。確かに機会の平等はあり得ても結果の平等がなくなるわけではないのです。「パレート最適」という気持ちの良さ（？）に惑わされてこれさえ達成すればよいと考えてはならない、とハテナ博士は思うのですが。

（参考：稲葉振一郎　『経済学という教養』）